11th LSI Design Contest in Okinawa
RSA Public Key Encryption System - 1/4
Takeo Yoshida
Hiroshi Ochi
1.Introduction
This year's design target is a RSA public key encryption CODEC. You may choose either Level 1 or Level 2 design specification depending on your skills. Enjoy RTL design and let us meet together at beautiful coral island Okinawa.
2.Basics
2.1 Some definition
Public key encryption algorithm has been developed by Rivest, Shamir, and Adleman in MIT as pioneers work. By taking their initial name, this algorithm is called RSA-encryption system. The RSA encryption algorithm is widely used such as for emails and files encryption system called PGP(Pretty Good Privacy) , for e-commerce encryption system called SSL(Secure Socket Layer) and so on.
In spite of widely used encryption algorithm, the RSA requires a lot of time for encryption and decryption of plane text. This is due to its heavy computational complexity since it makes use of prime factorization with respect to two prime number product.
This year's design target is to design an encryption or a decryption system with fewer computations(high-speed) and/or less number of gates as much as possible.
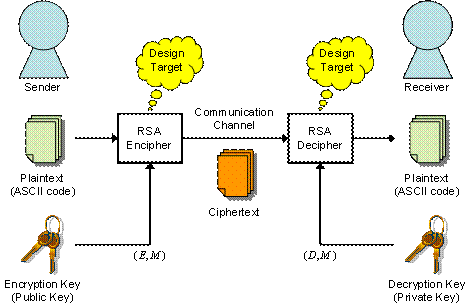
Fig. 1 RSA Encryption system
2.2 RSA Encryption Algorithm
Let us define some integer parameters P as a plane text, C as an encrypted text, E as the encryption key, D as the decryption key, and M as modulo number. The encryption can be made by following equation.
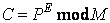 (1)
(1)
where mod expresses a modular operation.
On the other hand, the following equation is used for decryption.
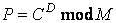 (2)
(2)
As we can see in Eq.(1) and (2), the RSA encryption system's expression itself is not complicated.
At the first step how to define E, D and M. we randomly choose quite large number of two prime factors p and q (p≠q). Then modulo M is defined as M=p×q. From p and q, we define
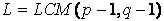 (3)
(3)
where LCM stands for the least common multiple.
The encryption key is chosen as a certain number which is less than and mutually prime with L. Therefore E can be expressed as
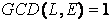 (4)
(4)
where GCD stands for the greatest common devisor.
In order to shorten the processing time(computational complexity), E is often chosen to be relatively small number.
Lastly, the decryption key D should satisfy the following equation for arbitrary integer number H.
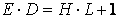 (5)
(5)
By using above defined E, D and M, encryption and decryption can be carried out according to the Eq.(1) and (2). See some references for more theoretical explanation.
As you might already realize it, the decryption key D can be easily obtained if the modulo M can be prime factorized; however, as far as M is chosen as several hundred digits, prime factorization would take more than several to 10 years or more even by using a state-of-the-art super computers. This ensures the robustness against attacking in terms of the RSA algorithm.
2.3 Examples
(1) Key generation
Suppose we choose p=11 and p=23, find the encryption key E, the decryption key D, and the modulo M.
[Answer]
M=p×q=253
L=LCM(11−1,23−1)=110
According to Eq(4), E satisfies GCD(L, E)=1; therefore, E=101 is one of the candidate.
If we choose H=56 as an arbitrary integer number, then D=61 according to Eq.(5).
(2) Encryption and decryption
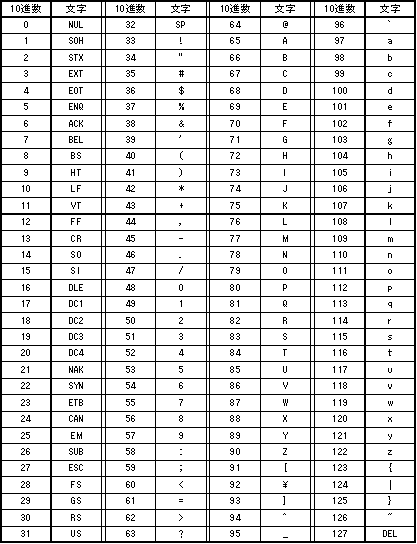
Suppose we make use of the ASCII code book, see Table 1, to convert Alphabet characters into certain integer numbers. Encrypt the following plain text into cipher text. Then decrypt this cipher text into the original plain text. Here we encrypt a plane text one character by one character. Normally, a block wise processing, which means several characters are encrypted as block manner, is used for it.
→ Plain text : Enjoy HDL!
[Answer]
According to ASCII code book in Talbe 1, we get
→ Coded plain text : 69 110 106 111 121 32 72 68 76 33
Applying Eq(1) into first character'E', which is 69 in ASCII code, we get
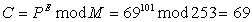
This number 69 is the encrypted code in terms of the first character 'E'. The problem in this equation is that heavy complexity is required for power calculation. The solution of this problem could be one of the goal for better RTL design.
As was same manner for the first character, the whole plain text can be encrypted as follows;
→ Encrypted(Cipher) text : 69 209 172 122 220 219 193 68 43 176
This cipher text can be decrypted by using Eq.(2). For the first encrypted data '69', we get
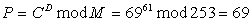
This is nothing but character 'E'as was in the original plain text.
Try to decrypt other cipher text all together.