1. ノイズ除去アルゴリズム

ノイズ除去の手法としては，複数のマイクロホンを用いて雑音を取り除くマイクロフォンアレー手法や 未知経路推定を行う適応フィルタリングを用いて雑音を取り除く手法等数多くの手法が提案されているが， 今回は周波数領域で雑音除去を行うスペクトル・サブトラクション法(SS法)を用いた雑音除去システムを実装する.
去年と異なるのは，1-1頁とは別に効率的なアルゴリズムを導入したことである．

1-1. スペクトルサブトラクション法

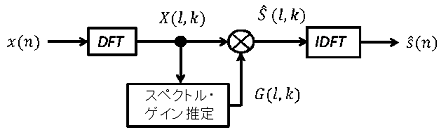
ここでは，雑音除去アルゴリズムについて説明する．本システムでは周波数領域での雑音除去を行う． 図1に雑音除去アルゴリズムの構成図を示す．

まず，観測信号が音声とノイズの和で与えられると仮定する．時刻nにおける観測信号，音声，ノイズを それぞれx(n)，s(n)，d(n)とする．このとき観測信号x(n)は次式で表せる．

ただし，音声とノイズは無相関であると仮定する．

次に，周波数領域での雑音除去のため，観測信号の離散フーリエ変換(DFT) を行う． DFT後の第lフレームにおける，フレームの先頭からk番目の観測信号スペクトルX(l,k)は次式で与えられる．

ただしS(l,k)，D(l,k)はそれぞれ音声と雑音のスペクトルである．ここで観測信号スペクトルX(l,k)から， 以下のように音声スペクトルの推定値を求めることを考える．

G(l,k)はスペクトルゲインであり，観測信号スペクトルに適当なスペクトルゲインを乗じたものが，推定信号スペクトルとなる． 理想的なは音声とノイズのスペクトルX(l,k)，D(l,k)を用いて，次式のように与えられる．

式(4)を式(3)に代入すると，理想的なスペクトルゲインとして，次式が得られる．

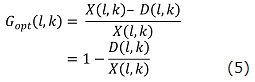
この時，音声スペクトルを完全に取り出すことができる．しかしながら，X(l,k)の情報だけでは雑音スペクトルD(l,k)を求めることはできない． そこで，SS法では非音声区間のL個のフレームを用いて，ノイズ・スペクトル推定値を次式で求める．

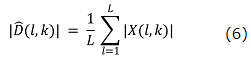
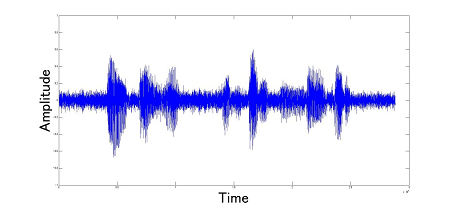
SS法をScilab上でシュミレーションした結果を以下に示す． プログラムファイル (SS_Method.zip)はここからダウンロードできる．

1-2. 可変音声分布を利用したMAP推定法

本年度新たに導入するアルゴリズムである．それに伴い7.ダウンロード内の"DL_file_ver3.zip"には関連するファイル(MAP_Method.zip)を同梱している．

1-2-1. MAP推定法

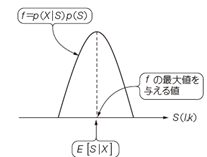
MAP推定では次式により音声スペクトルの推定値を得る．

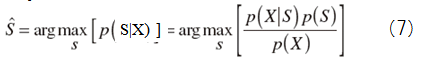
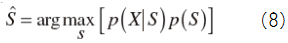
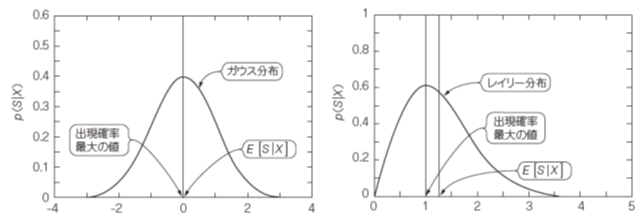
ウィーナー・フィルタのMAP推定値を得るために，音声スペクトルSとノイズ・スペクトルDのPDFが，いずれも次のガウス分布で与えられると仮定する．

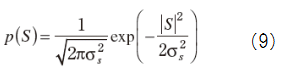
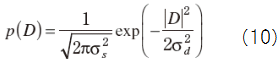
X＝(定数)＋Dと考えることができる．ノイズDの発生確 率がSに無関係であるとすると，

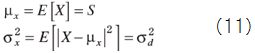
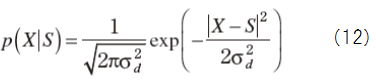
εを次のように定義し，このεを最大にするSを求める．

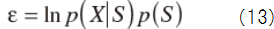
Sは次のように書き換えられる．

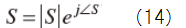
振幅｜S｜と位相∠Sが統計的に独立であると仮定する．このとき

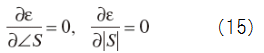
をそれぞれ解くことで，音声スペクトルの推定値を次のように得る．

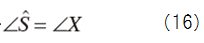
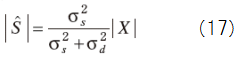
(16),(17)式より

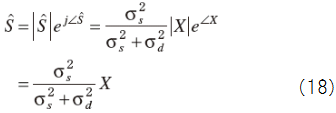
よって，次のスペクトルゲインが得られる．

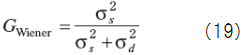
ここで，γ，ξを次のように定義する．

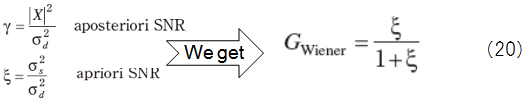
・Decision-Directed法

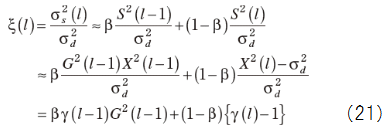
βは平均をとる割合を決める定数であり，標準的には0.98が用いられる．また，右辺最後の{γ(l)?1}が負とならないよう，実際には次式を用いる．

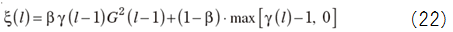
・MAP推定法

ほとんどの音声信号はガウス分布よりもレイリー分布に従う．

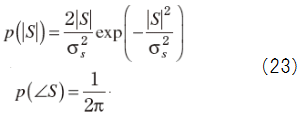
ノイズについては実部と虚部が無相関でそれぞれ半分ずつの分散を持つガウス分布に従うと仮定すると，次式のようになる．

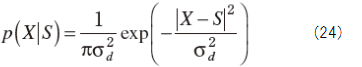
音声の振幅および位相スペクトルに対して(13)〜(19)式の手順でMAP推定を行うと，次のスペクトルゲインが得られる．

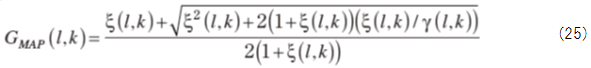
l，kはそれぞれフレーム番号，スペクトル番号である．

1-2-2. T.LotterとP.Varyの音声スペクトル分布

T.LotterとP.Varyによって提案された音声スペクトルのPDF(確率密度関数)は有用なものの一つである．

彼らによると，位相スペクトルは一様分布，振幅スペクトルは次の関数で近似表現できる．

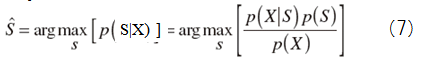
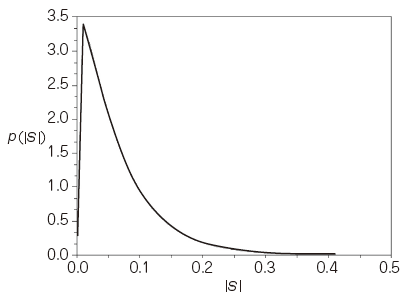
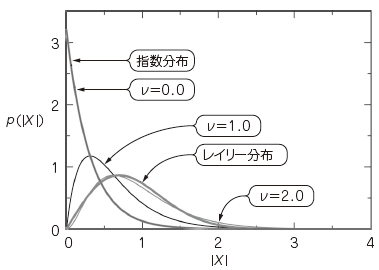
Γ(・)はガンマ関数であり，μ，νは分布の形状を決めるパラメータである．式(7)で与えられるPDFを図3に示す．

Lotterらの分布を用いてMAP推定値を求めれば，次のスペクトル・ゲインが得られる．

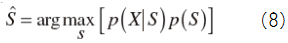
ただし，l，kはそれぞれフレーム番号，スペクトル番号であり，

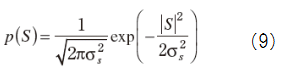
である．本方式において，位相スペクトルのMAP推定値は，観測信号の位相スペクトルに一致することが示されている．

1-2-3. 可変音声分布

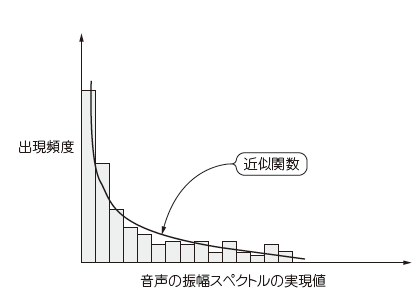
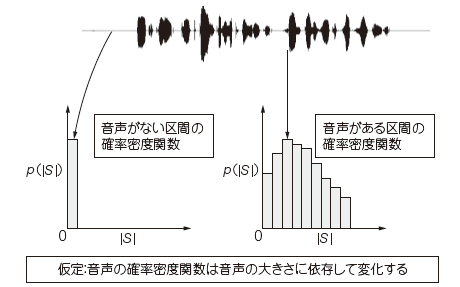
Lotterらによって提案された分布関数は，パラメータを固定値としているため，そのPDFの形状は常に一定である． しかし，実際の音声には，休止区間や，音声の始まりや終わり付近に見られる小さいレベルの音声成分も多く含まれている． そして，これらの区間においては，音声振幅スペクトルのPDFは，0だけが出現するデルタ関数か， または指数分布に近い形となるはずである．一方，音声が存在する区間だけに注目すると， 音声振幅スペクトルのPDFは，レイリー分布に近い形状となることが確認されている．音声PDFが変化する様子を図5に示す．

音声スペクトル分布の形状を，音声区間と非音声区間で適応的に変化させる方法を，ここでは可変音声分布(variablespeechPDF)方式と呼ぶ．

Lotterらによって導かれた式(7)は，パラメータνのとり方によって，指数分布からレイリー分布までを近似できる． この様子を確認するため，νを変化させた場合に式(7)が与える分布曲線を図6に示す．ただし，μ＝3.2に固定している．

式(7)は，ν＝0.0のときに指数分布に一致し，ν＝2.0のときはレイリー分布に近似する．つまり，非音声区間ではν→0.0とし，音声が存在する区間ではν→2.0とすれば実際の音声PDFの変化を近似できると考えられる．

可変音声分布に基づくスペクトル・ゲインは，Lotterらのスペクトル・ゲインのパラメータを可変にすることで得られる．

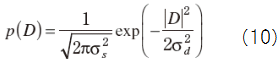
ここで，可変音声分布を実現するν(l,k)は各フレームの音声の大きさをSNRで評価して決定する．ν(l,k)を決定するためのアルゴリズムは次式で与えられる．

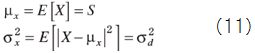
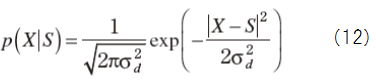
ここで，NはFFTスペクトルの数(フレーム長と同じ)であり，αはν~(l,k)の大きさを調整するパラメータである．式(11)と式(12)から分かるように，ν~(l,k)は，観測信号スペクトル全体の事後SNRに基づいて適応的に変化する．

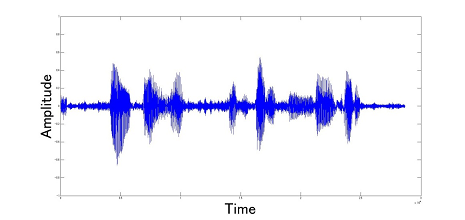
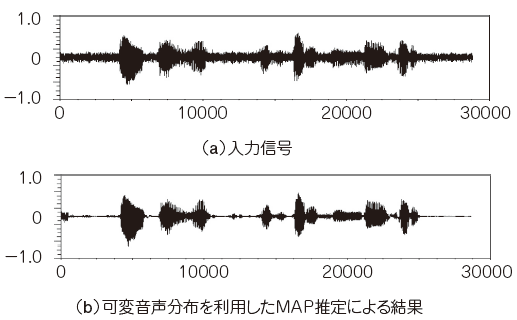
可変音声分布を利用したMAP推定法をScilab上でシミュレーションした結果を以下に示す．プログラムファイル(MAP_Method.zip)はこちらのDL_file_ver3.zipに同梱されている．