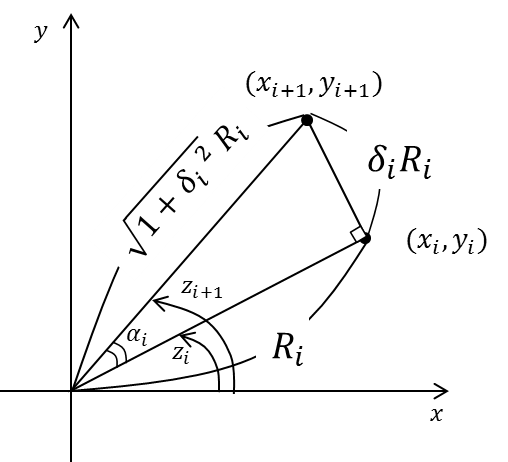3-1. CORDIC法([1])

CORDICとは，初等関数の値を計算する1つの方法であり，平面でベクトル（あるいは座標）を回転させながら計算を行う．

最終的に求めたい角度を\(θ\)として，図1ではCORDIC法における\(cosθ\)，\(sinθ\)の求め方の概要図を示している．図1に示すように， CORDIC法は角度\(z\)が角度\(θ\)に近づくように処理を繰り返すことで，座標\(x\)を\(cosθ\)として，座標\(y\)を\(sinθ\)として算出する． また図1より，角度\(z\)には次のような関係がある．

式(1.1)は角度\(θ\)に近づいていくために，角度\(α\)を角度\(z\)に加えていくことを示している．このときそれぞれの角度間は次のような関係となる．

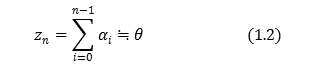
式(1.10)で示すように，角度\(z\)は最終的に\(θ\)へ近づく．このようにして\(sinθ\)，\(cosθ\)を求める．続いて，CORDIC法の主な原理について説明する．

図2ではCORDIC法において角度\(z\)をどのようにして角度\(θ\)に近づけるかを示している．まず座標\(x_i\)，\(y_i\)と原点とを結ぶ線分の長さを\(R_i\)， その角度を\(z_i\)とすると，座標\(x_i\)，\(y_i\)および角度\(z_(i+1)\)は以下の式で表される．

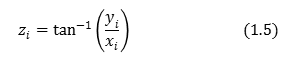
ここで角度\(z_i\)を角度\(θ\)へ近づけるための更新値\(α_i\)を考える．

式(1.6)のように定義すると\(sinα_i\)，\(cosα_i\)は以下のようにあらわせる．

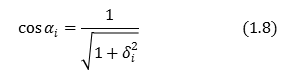
式(1.7)，(1.8)を用いることにより，点\((x_i,y_i)\)から\((x_(i+1),y_(i+1))\)への座標変換を次のように表すことができる．

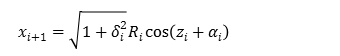
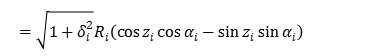
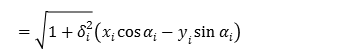
同様にして，

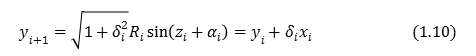
続いて，例として\(cosθ\)，\(sinθ\)がどのように計算されていくのか，過程を追ってみていく．

ここで図3に示すように，回転していくベクトルの初期位置がx軸上にあるものとし，初期座標点を\((x_0 ,y_0 (=0))\)とする．\(z_n＝θ\)とすると,

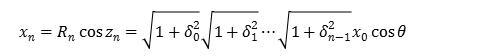
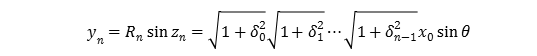
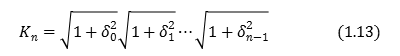
式(1.11)，(1.13)から\(x_0\)の初期値を決めてn回の回転後の\(x_n\)座標と\(y_n\)座標とを求めれば，与えられた角度\(θ\)の\(cosθ\), \(sinθ\) は以下のように求めることができる．

注意しなければならない点として，回転をn回繰り返して角度\(z_n\)が角度\(θ\)に近づいたものとし，\(θ\)を誤差とすると，

式(1.16)のように，n回繰り返しても誤差が発生してしまうことがある．