3-1. CORDIC method([1])

The CORDIC, it is one way to compute the value of the elementary functions, the calculation is performed while rotating the (or coordinates) vector plane.

\(θ\) as the angle to be obtained finally, shows a schematic diagram of a method of determining the \(sinθ\) and \(cosθ\) in the CORDIC method in Figure 1. As shown in Figure 1, CORDIC method by repeating the process angle \(z\) is to approach the angle \(θ\), \(cosθ\) as the coordinates \(x\), is calculated as \(sinθ\) the coordinates \(y\). Also from Figure 1, there is a relationship, such as the following angle the \(z \).

To approaches the angle \(θ\), (1.1) shows that it will add to the angle \(Z\) angle \(A\). At this time, the angle between each of the relationship, such as the following.

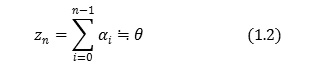
As shown in (1.10), the angle \(z\) is closer to \(θ\) eventually. To determine \(sinθ, cosθ\) in this way. The following will describe the main principle of the CORDIC method.

Shows the how the angle \(z\) whether the angle \(θ\) closer to the CORDIC method in Figure 2. I to R the length of the line segment connecting the origin (\(x_i\), \(y_i\)) coordinates first. I and z the angle at that time. Coordinates (\(x_i\), \(y_i\)) and angle z_i+1 is expressed by the following equation.

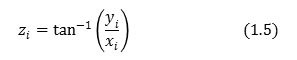
Consider the update value \(α\) to approximate to the angle \(θ\) the angle \(z\) here.

When defined by the equation (1.6), \(sinα_i\) and \(cosα_i\) can be expressed as follows.

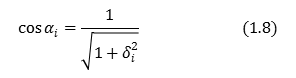
By using (1.7), (1.8) equation, it can be expressed as follows: coordinate transformation \((x_(i+1),y_(i+1))\) to the point from \((x_i,y_i)\) point.

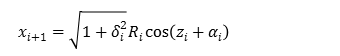
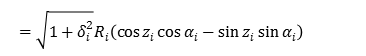
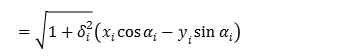
Similarly,

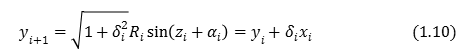
Then, how \(sinθ\) and \(cosθ\) or go is calculated as an example, or try to follow the process.

As shown in Figure 3，It is assumed that the x-axis on the initial position of the vector will rotate，Initial coordinates point is \((x_0 ,y_0 (=0))\)．Assuming that \(z_n＝θ\),

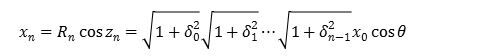
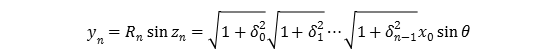
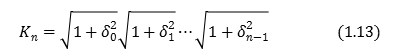
In determining the initial value of \(x_0\) from (1.13) and (1.11), by obtaining the \(x_n\) and \(y_n\) coordinates after the rotation of \(n\) times， \(sinθ\) and \(cosθ\) of the angle \(θ\) given can be determined as follows.

Attention must be paid to, It is assumed that the angle \(z_n\) approaches the angle \(θ\) by repeating n times the rotation, Assuming that the error \(θ\)，

As (1.16), there is an error occurs even after repeated \(n\) times.