| Japanese | English |

Design Specification
1. Purpose2. Design enviroment
3. Principle
3-1. CORDIC method
3-2. Extension to \(-ÉőĀ`Éő\)
3-3. Algorithm
4. Design
4-1. Design of the updated
value \(ÉŅ_i\) and \(ɬ_i\)
4-2. Judgement of the angle \(z\)
by the angle \(É∆\)
4-3. Determination of the
initialvalue \(x_0\)
4-4. Output example of the
value
5. Example to Level2
6. Challenge
7. Unit of measurement of the
circuit scale and speed
18th LSI Design ContestsĀEin Okinawa Design Specification - 4-5
4-5. Output example of the value
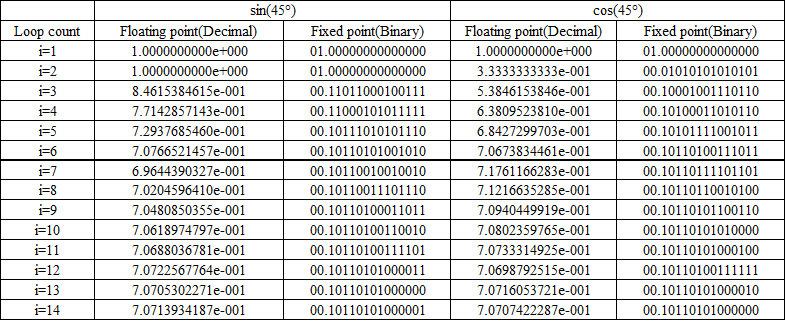
When finding the cosÉ∆ and sinÉ∆ using the CORDIC method, an example \(cos45Āč\) and \(sin45Āč\), to see how they approached.
First, in order to ensure that the value is approaching shows true value of \(cos45Āč\) and \(sin45Āč\)ĀD This is represented by a fixed-point and binary floating point decimal.
Also, a result of output in a C program for output of these values, the verification environment is Microsoft VisualStudio2010.
Next, Table 2 shows the values of the \(cos45Āč\) and \(sin45Āč\) as determined by the CORDIC methodĀD
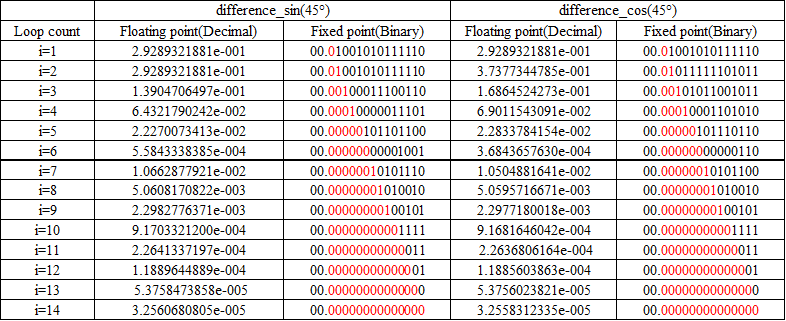
From Table2, It is seen that approaches the true value of Table 1 by increasing the number of loopsĀD At this time, Are summarized in Table 3 which took the difference between the calculated value of the CORDIC method and the true value for each loop.
In Table 3, As you look at the things that were expressed in fixed-point, it shows the accuracy of the CORDIC method obtained by subtractionĀD At the location where it was displayed in red. Some errors exist, but the accuracy of each loop is almost obtainedĀD However, the results obtained, since it depends on the execution environment, the result is only an exampleĀD
I is shown in Table 4 that represents how an operation is whether advances in CORDIC.
I can be seen that the calculation is performed repeatedly on the basis of the determination of \(z\) from Table 4, is approaching gradually to the angle \(É∆\). The z determination at this time is determined relative to the z obtained in the calculation of the previous one.