第11回LSIデザインコンテスト・イン沖縄 設計仕様書 - 2/8
3.RSA暗号の全体像
さて前置きが少し長くなりましたが、ここから本題であるRSA暗号の説明に入ります。 上では説明しませんでしたが、公開鍵暗号では、公開している暗号化鍵から、秘密にしている復号鍵を容易には求められない仕掛けが必要になります。この仕掛けを初めて実現した、世界初の公開鍵暗号がRSA暗号です。RSA暗号は、MIT(マサチューセッツ工科大学)に勤務していたRivest、Shamir、Adlemanの3名の研究者によって開発されたので、この3名の頭文字をとってRSAと命名されました。RSA暗号は、コンピュータを使う人であれば、誰でも、知らないうちに使っている可能性があります。そのくらい、現在までに広く実用化されています。具体的には、電子メールやファイルの暗号化に用いられるPGP(Pretty Good Privacy)や電子商取引などに用いられるSSL(Secure Socket Layer)などがあります。また詳細は割愛しますが、RSA暗号は、電子署名を実現することもできます。 このように、広く普及しているRSA暗号ですが、その暗号化・復号の処理では、非常に大きな値を扱うため、処理時間が長くなるといった問題点もあります。そのため、暗号化・復号を行うハードウェア製品も多数販売されています。今回の課題は、RSA暗号の暗号化・復号を行う回路を実現することです。このRSA暗号を一言で説明すると、二つの素数の積を求める手間に比べて、その積を素因数分解する手間の方がとても難しく時間がかかるという性質を利用した暗号、ということになります。何やら難しそうな印象を受けるかも知れませんが、RSA暗号の暗号化と復号の手順は、非常に単純です。 いま、平文P、暗号文C、暗号化鍵E、復号鍵D、法Mのそれぞれが、正整数で表されているものとします。このとき、RSA暗号では、以下の式を用いて、暗号化を行います。
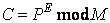 (1)
(1)
ここで、mod は剰余を求める演算子で、AmodBは、AをBで割った余りを表します。またRSA暗号では、以下の式を用いて、復号を行います。
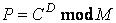 (2)
(2)
以上のように、RSA暗号における暗号化・復号の式は、非常に単純な式となっています。 次に、暗号化鍵E、復号鍵D、法Mの作り方を説明します。まず、非常に大きな二つの素数p、q(p≠q)をランダムに選びます。このとき、法M=p×qとします。次にp、qから、
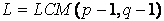 (3)
(3)
を求めます。ここで、LCM(a,b)は、aとbの最小公倍数を表します。このとき、上記のLと互いに素、かつ、L未満となる数を選び、その数を暗号化鍵Eとします。すなわち、暗号化鍵Eは、
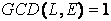 (4)
(4)
を満たす、L未満の数とします。ここで、GCD(a,b)は、aとbの最大公約数を表します。なお、暗号化の処理時間を短く済ませるために、暗号化鍵Eには、小さな値がよく用いられます。さらに、復号鍵Dは、ある正整数Hに対して、以下の式を満たす数とします。
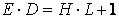 (5)
(5)
以上の方法で得られる暗号化鍵E、復号鍵D、法Mを用いれば、先に示した式(1), (2)を用いて、暗号化と復号を行えます。これらの式(1), (2)を使って暗号化および復号を行えることの理論的な背景については割愛しますが、次節で暗号化および復号の具体例を示すことにします。なお、RSA暗号では、法Mと暗号化鍵Eを公開しておき、復号鍵Dを秘密に保持しておきます。 ところで先ほども説明しましたが、RSA暗号では、素因数分解の難しさを利用して、第三者が暗号文を解読することを困難にしています。鍵や法の作り方からもわかると思いますが、RSA暗号では、法Mを素因数分解できれば、簡単に復号鍵Dを求めることができてしまいます。しかし、法Mの桁数が数百桁以上になる場合、その素因数分解に要する時間は、最新のコンピュータを使っても数年から数十年以上の単位になってしまいます。すなわち、RSA 暗号を実際に使用する場合、できるだけ桁数の多い鍵と法を用いる必要があります。 以上がRSA暗号の全体像になります。
