第11回LSIデザインコンテスト・イン沖縄 設計仕様書 - 4/8
5.RSA暗号化器のハードウェア実装に関する注意点
設計課題のシステム概要を図4に示します。課題は、RSA暗号の暗号化器と復号器の設計です。とは言っても、式(1)と式(2)を比べるとわかると思いますが、RSA暗号の暗号化器と復号器は同じになります。ですから実際は、暗号化器(復号器)のみを設計すれば良いことになります。
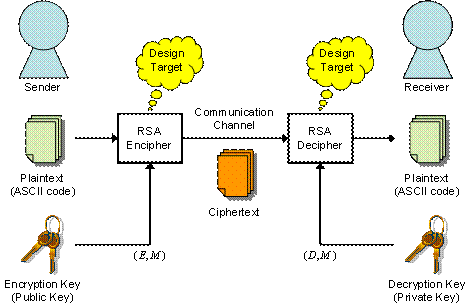
図4 設計課題のシステム概要
ここでは、式(1)を実現する回路を設計する際の注意点を述べておきます。式(1)は、非常に単純な式ですが、式(1)で用いられている2種類の演算、すなわち、べき乗の計算とmod演算は、どちらも論理合成できない演算です。今回の課題では、これらの演算をどのように実現するのかがポイントになります。以下では、これらの演算を、論理合成可能な演算子だけを用いて実現する方法を示します。 まず、べき乗の計算方法から説明します。式(1)を言葉で説明すると、「暗号文Cは、平文PをE乗し、その結果をMで割った余り」となります。すなわち、C<Mが成り立ちます。もちろん、同様に、P<Mも成り立ちます。しかし、途中結果である「平文PをE乗」した結果は、非常に大きな値になります。先ほどの暗号化の例に登場した69101は、10進数で200桁近い値になります。たった1文字を暗号化するために、このように大きな値を回路内部に保持することは、現実的ではありません。ですから、この計算には工夫を要します。幸い、mod演算では、
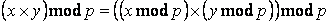 (8)
(8)
という等式が成り立ちます。すなわち、複数の数を掛けてから、最後にmod演算をする場合、途中でmod演算を施しても、計算結果は同じになります。この式を用いて、例えば、下式のように、乗算を行うたびに剰余を計算しておけば、途中の計算結果が非常に大きくなることを防げます。
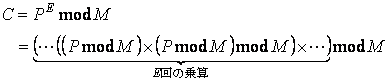 (9)
(9)
この例では、計算の途中結果がM2をを超えることはありません。しかし、この方法では、E回の乗算が必要になります。先ほどの暗号化の例でさえ、101回もの乗算が必要になってしまいます。安全性を考慮した実用的なサイズの暗号化鍵Eを用いる場合は、101とは比較できないほど大きな数を用いますので、さらに非現実になってしまいます。ですから、もう一工夫する必要があります。ここでは、よく用いられる工夫を説明します。
まず、10進数表現の暗号化鍵Eを2進数を使って、
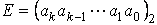 (10)
(10)
のように表します。ここで、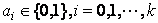 です。このとき、
です。このとき、
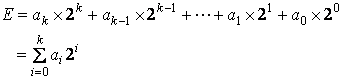 (11)
(11)
となります。この式を用いると
 (12)
(12)
と表せます。さらに、式(9)と式(12)を用いると、
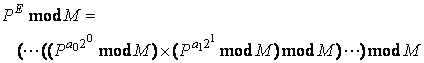 (13)
(13)
となります。つまり、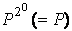 の計算、
の計算、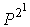 の計算、…、
の計算、…、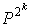 の計算と続けていき、必要に応じて、それらを掛け合わせればよいことになります。ここで、「必要に応じて」とは、
の計算と続けていき、必要に応じて、それらを掛け合わせればよいことになります。ここで、「必要に応じて」とは、
 (14)
(14)
となるので、「ai=1のときだけ掛ければよい」という意味です。また、式(13)において、乗算のたびにmod演算を行っておけば、途中の計算結果はM2を超えることはありません。
ここで、肝心の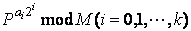 は、
は、
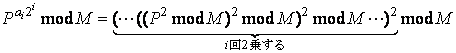 (15)
(15)
のように、i回の2乗とmod演算で計算することができます。
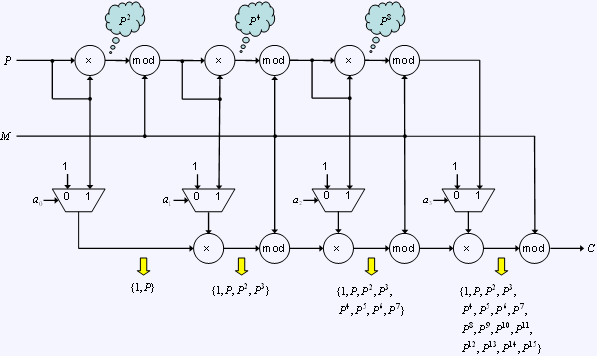
数式がたくさん登場しましたが、結局のところ、式(13)と式(15)を用いれば、式(1)を計算できることになります。このとき、途中結果の値は、M2を超えません。また、乗算やmod演算の回数も、Eの値そのものではなく、その桁数(Eのlogオーダー)に比例した回数で済みます。図5に、式(13)と式(15)を用いた場合の暗号化の流れを示します。図5を見ると、規則的な流れになっていることがわかると思います。以下、この流れについて説明します。
まず、図5の例では、暗号化鍵の長さを4ビットとし、E=(a3,a2,a1,a0)2と表しています。鍵の長さが4ビットなので、最大P15を計算する必要があります。図5の上側では、最初に、P×P=P2を求め、次に、P2×P2=P4を求め、最後に、P4×P4=P8を求めていることがわかります。
すなわち、式(15)にしたがって、 P2, P4, P8を次々に計算しています。もちろん、乗算のたびに、mod演算をしていますので、途中の計算結果はM2を超えません。一方、図5の下側では、最初に、1×1(=1)、P×1(=P)のいずれかの計算を行っています。どちらの計算を行うのかは、式(14)にしたがって、a0の値で判断します。実際には、この乗算は1を掛けるだけの無意味な計算なので、図5では乗算とmod演算を省略していますが、便宜上、このように説明しています。次に、この結果に対して、1またはP2を掛けています。どちらを掛けるかは、同じく式(14)にしたがって、a1の値で判断します。この結果は、a0とa1の値の組み合わせによって、1,P, P2, P3のいずれかになります。以下同様に、1またはP4を掛け、その結果に、1またはP8の結果を掛けます。このような手順で計算すると、E=(a3, a2, a1, a0)の値に応じて、P0(=1), P1(=P), P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, P12, P13, P14, P15のいずれかの値が計算され、mod演算の後、暗号文Cとして出力されます。なお、暗号化鍵の長さが長くなった場合でも、乗算とmod演算の回数が増えるだけで、すなわち、図5が右方向に伸びるだけで、基本的な構造は同じままで暗号化ができます。
次に、modの計算方法について説明します。mod演算のアルゴリズムやハードウェア化の方法には、さまざまな方法があります。また、加算の後のmod演算や乗算の後のmod演算など、特定のケースでmod演算を行う場合、それに特化して高速化を行う方法もあります。ここでは、凝った方法の紹介は割愛し、単純な方法を一つだけ紹介しておきます。
mod演算は、剰余(割った余り)を求める演算なので、結局は、割り算(除算)を行うことで求められます。ですから、結果がB未満になるまで、AからBを引き続ければ、A mod B を計算することができます。しかし、この方法は、式(9)でべき乗を計算するのと同様に、非常に効率が悪くなるので、やはり、工夫が必要になります。
ここで登場するのが、小学校で習った筆算による割り算です。筆算による割り算とは、紙に数字を書いて、割り算を計算する方法です。例えば、12345÷171を計算する場合、図6に示すように、まず「?」の部分がいくつになるのかの見当をつけます。試しに、「?」を8として計算すると、余りが-134となってしまい、仮定した値が大きすぎることがわかります。そこで今度は、「?」を7として計算すると、今度はうまくいくので、次の桁の見当に移ります。このように、筆算の割り算では、商の値を仮定し、それに除数を掛けた値を、被除数から引く、という手順を繰り返します。なお、図6の計算を最後まで行うと、図7に示すように、12345÷171の結果は、商が72、余りが33となります。
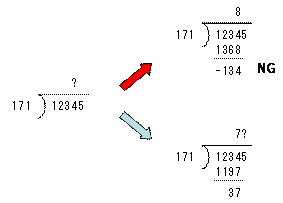
図6 10進数の割り算

図7 12345÷171の結果
さて、ディジタル回路の内部では、通常、2進数が扱われます。今回の課題では、この2進数同士の割り算をする回路を設計する必要があります。この割り算回路を実現する上で、筆算による割り算の手順が役に立ちます。図6に示したように、10進数の割り算の場合、仮定する商は、0〜9までの10通りあります。しかし、2進数での割り算の場合、0または1の2通りしかありません。すなわち、引けるか、引けないか、だけを考えればよくなり、10進数の割り算よりも単純になります。例えば、2進数の割り算11011110÷1010を、筆算で行うと、図8のようになります。
図8で行われている処理は、引けるか、引けないかを判断するための大小比較、次の桁に移る処理、引き算の三つです。これらの処理を、桁数に比例した回数繰り返すことによって、割り算を行うことができます。なお、これら三つの処理は、いずれも論理合成できます。

図8 2進数の割り算
以上で、一応、論理合成可能な演算子のみを用いて式(1)を実現できることがわかって頂けたと思います。しかし、以上で説明した計算方法は、あくまでも一例ですし、改善の余地がたくさん残されています。そこで、残された改善の余地について補足しておきます。
まず、べき乗ですが、これは図5にしたがって計算することが可能です。例えば、図5をそのままハードウェア化することも可能です。この場合、使用される構成要素は、乗算器、セレクタ (マルチプレクサ)、mod演算器の三つです。mod演算器に関しては後で説明しますが、残りの乗算器とセレクタは、HDLで簡単に記述でき、論理合成も可能です。ここで注意する必要があるのは、乗算器です。VHDLでも、Verilog-HDLでも、乗算の記号は「*」です。この記号「*」は、合成可能ですが、非常に大きな回路が合成されます。今回の課題であるRSA暗号化器では、通常、1000ビットとか2000ビットといった非常に大きな数が扱われますが、このように大きな数の乗算にそのまま「*」を用いても、コンピュータの処理能力上、まず合成できないでしょう。仮に合成できたとしても、その回路は使い物にはなりません。今回の課題では、1000とか2000ビットといった大きな数は扱わないので、「*」の使用も可能ですが、課題に取り組む際には、この点を念頭に置き、余力があれば改善して下さい。
これと同じようなことが、mod演算器の大小比較でも言えます。先ほど説明した手順をmod演算器に適用する場合、引けるか、引けないかを判断するための大小比較器が必要になります。HDLでは、関係演算子を使って大小比較をすることが可能であり、合成もできます。しかし、大きな数同士の大小比較は、効率が良いとは言えません。除算器について調べてもらえればわかると思いますが、実際には大小比較を行わず、いきなり引き算をします。この先の対処方法、すなわち、引き算の結果が負であった場合の対処方法には、二種類あります。一つは、引いた値を足して、元に戻してから、次の桁に移る方法です。もう一つは、そのまま次の桁に移り、その桁では引かずに足す、という方法です。それぞれ、引き戻し法、引き放し法と呼ばれています。ここではこれ以上触れませんが、mod演算器を設計する際の参考にして下さい。もちろん、今回の課題で扱う数はそれほど大きくないので、関係演算子を使用することも可能です。しかし、余力があれば、この点についても改善を試みて下さい。
RSA暗号化器を設計する場合、通常、非常に大きな数を扱いますが、そのように大きな数をどのように処理するのかがポイントになります。上では、乗算器と大小比較器についてのみ述べましたが、本当は、加算や減算についても、算術演算子をそのまま使用するのは好ましくありません。このように見ていくと、多くの改善点があることがわかると思います。課題に取り組む際の参考にして下さい。