第11回LSIデザインコンテスト・イン沖縄 設計仕様書 - 3/8
4.RSAによる暗号化と復号の例
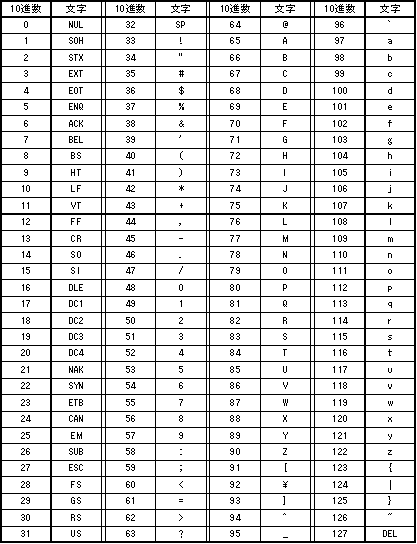
次に、RSA暗号の暗号化と復号の具体例を示します。そのためには、まず、暗号化鍵E、復号鍵D、法Mを決めておく必要があります。そこでまず、二つの素数p、q(p≠q)を選びます。ここでは、それぞれ二桁程度の数とし、p=11、q=23としておきます。これらの素数から、法M=p×q=253となります。また、L=LCM(11−1,23−1)=110となるので、暗号化鍵Eとして、101を選ぶことにします。実際に、GCD(110, 101)=1となることを確認してみて下さい。次に、これらの数を式(5)に代入し、H=1,2,3,…について、整数になるDを探すと、H=56のとき、D=61となることが分かります。以上で、暗号化鍵E、復号鍵D、法Mが決まりました。この他に、平文の表現に用いる文字コードとブロックサイズの値を決めておく必要があります。ここで、ブロックサイズとは、一度に暗号化を行う文字数のことです。通常、平文の文字数は膨大になります。そのため、平文の内容をいくつかのブロックに分け、個々のブロックについて式(1)を用いて暗号化を行います。このときの一つのブロックの文字数がブロックサイズになります。このブロックサイズも大きな値にする必要がありますが、以下では簡単のために、1文字ずつ暗号化するものとします。また、平文に使用する文字コードですが、今回は、ASCIIコードが使用されているものとします。なお、ASCIIコード表を表1に示しておきます。 以上で準備ができたので、RSA暗号の暗号化と復号の例を見てみましょう。まず、平文の例を示します。
» 平文の例 : Enjoy HDL!
表1のASCIIコード表から、上記の平文を文字コードで表現すると、以下のようになります。
» 平文の文字コード表示 : 69 110 106 111 121 32 72 68 76 33
ここで、平文の最初の文字‘E’をASCIIコードで表すと69になります。これを式(1)に代入すれば、暗号化された文字の文字コードが得られます。すなわち、
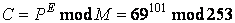 (6)
(6)
を計算すればよいわけです。しかし、PEの結果は、桁数が非常に多くなるため、筆算や普通の電卓では計算できないと思います。幸い、この程度の桁数であれば、ちょっとしたプログラムを作ったり、桁数の多い数を扱える電卓ソフト等を使えば、比較的簡単に計算結果を確認できます。これらの方法で確認した結果,式(6)の結果はたまたま同じ69となりますが、以下のような暗号文が得られました。
» 暗号文の文字コード表示 : 69 209 172 122 220 219 193 68 43 176
また、この暗号文を平文に戻すには、式(2)を使います。例えば、暗号文の最初の文字69を復号するには、
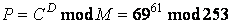 (7)
(7)
を計算すればよいわけです。式(7)の結果は69になります。残りの文字についても、暗号化の計算と同じようにして確認したところ、元の平文の文字コードが得られました。