第13回LSIデザインコンテスト・イン沖縄 設計仕様書 - 2
2.送信ビットの生成方法
送信回路や受信回路のシンドローム計算回路では多項式を割り算し余りを求める回路が必要になりますので、多項式を用いた説明を以下行います。
7ビットの情報ビットを{u0, u1, u2, u3, u4, u5, u6 }とし、以下の多項式U(x)で表します。ここで多項式を用いていますが、変数xを解くような意味はなく、Xnがそのビットの位置を表しています。
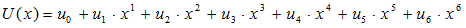 … (1)
… (1)
そうすると、15ビットの送信ビットは以下のような多項式SB(x)で示すことができます。
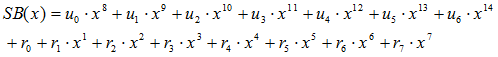 … (2)
… (2)
これを表で示すと、以下の表2のようになります。表2からもわかりますが、情報ビットを右側に配置しましたので、Xの時数8次から14次の部分の情報ビットが割り当てられ、0次から7次にエラー訂正用のパリティビットが割り当てられています。
表2 情報ビット(7ビット)と送信ビット(15ビット)と多項式係数

すなわち、
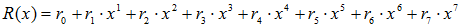 … (3)
… (3)
を求めれば、U(x)が与えられているので、容易にSB(x)を生成することが可能となります。実はR(x)は以下の(4)式を(5)式で割り算を行った余りとなります。ここで、G(X)のことを生成多項式と呼びます。
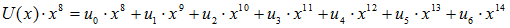 … (4)
… (4)
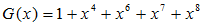 … (5)
… (5)
(4)式はU(x)にX8をかけたものですが、このX8をかけることにより、情報ビットが上位に8ビットシフトしたことになります。すなわち、デジタル回路でのnビットシフト処理は、ガロア多項式ではXのn乗の乗算にあたることになります。
(5)式の次数は8次なので、(4)式を(5)式で割った余りは7次式以下の次数となり、(3)式のR(X)の次数と合います。但し、ガロア体という普通の数学ではない割り算の余りを求めることになりますが、ガロア体での多項式の余りを求める方法は実は単純であり、
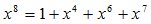 … (6)
… (6)
を用いて、8次の項を7次以下の式への変換を繰り返し用いることで、(4)式の次数を7次以下に下げるように変換することで求めることができます。但しこのとき、係数どうしの加算や減算はEXORで代用します。すなわち、
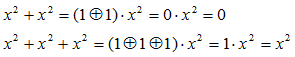 … (7)
… (7)
のように計算します。
