第13回LSIデザインコンテスト・イン沖縄 設計仕様書 - 4
4.解読器(DECODER)のアルゴリズム
さて、いよいよDECODERの仕様を説明します。ここでは、アルゴリズムの詳細は説明せず、どのような演算をもちいればエラー訂正できるかという方針で、説明を行います。今回の課題であるBCH(15,7)符号では以下の生成多項式を用いました。
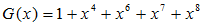 … (5)
… (5)
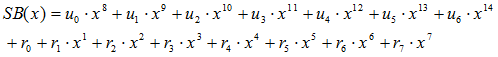 … (2)
… (2)
すなわち、符号を示す多項式SB(x)は、(2)式の形をしているので、生成多項式G(x)で割るとあまりが0となる性質を持っています。すなわち、割り算のあまりを計算して0であれば、エラーがないと判断することができます。
BCH(15,7)符号ではデータが7ビット、冗長(パリティ)ビットが8ビットで、15ビットの符号中2ビットの誤り訂正が可能な符号です。
以下(9)式に示すように、生成多項式G(x)は
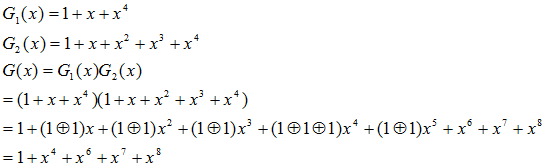 …(9)
…(9)
となり、G1(x)とG2(x)の積です。したがって、SB(x)はG1(x)でも、G2(x)でも割り切れることになります。すなわち、エラーがなければ、2つの余りは0となります。
送信信号SB(x)を送信して、RB(x)なる信号を受信したとします。送信中にエラーがなければ、RB(x)はSB(x)と同一であり、RB(x)をG1(x)もしくはG2(x)で割ると余りは0となります。もし送信中にエラーが発生すると、RB(x)をG1(x)もしくはG2(x)で割った余りは0ではなく、エラーの発生を検知することができます。
このRB(x)をG1(x)で割った余りをS1(x)シンドロームとし、G2(x)で割ったあまりをS2(x)シンドロームとすると、S1(x)およびS2(x)は以下のような3次の多項式となります。
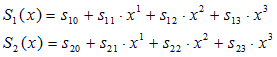 …(10)
…(10)
2つのシンドロームビット(S10, S11, S12, S13)と(S20, S21, S22, S23)の計8ビットにより、エラーのあるなし、エラー訂正可能かどうか、エラー訂正可能な場合に、反転すべきビット位置はどの位置かを知ることができます。ここでは、複雑なアルゴリズムでの解法はあきらめ、テーブルでの実装をします。というのも、シンドロームはすべてで8ビットであり、256通りの場合しかなく、TableすなわちROM等で実装が可能だからです。
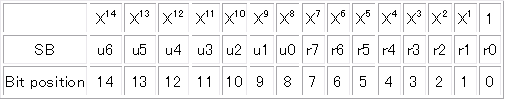
表5にシンドロームとエラー位置の関係を示します。黄色のセルはシンドロームがともに0の場合に対応しており、エラーのない場合で、Noneと表示されています。青色のセルは1ビットエラーに対応しており、符号語15ビットのエラーの位置15通りを示しています。エラー位置は表6に示すように、(2)式のXの指数と合わせています。赤色のセルは2ビットエラーに対応しており、15*14/2=105通りのパターンを示しています。各セルには2つの数値がしめされており、これらが2ビットエラーの位置に対応します。他のセルは3ビット以上のエラーがあり、エラー訂正不可能の状態を示しています。エラー発生は検知したが、訂正できない状態で135通りあります。
表5 シンドロームとエラー位置の対応表
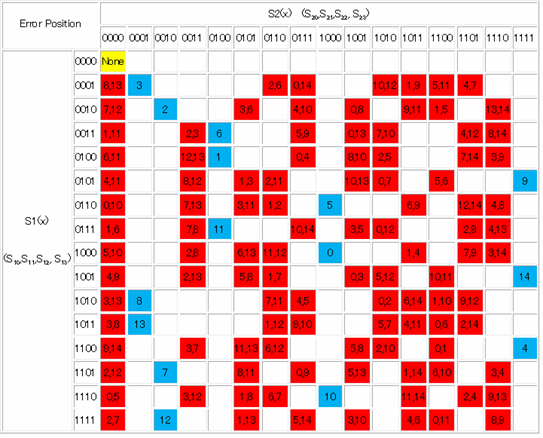
表6 エラー位置の対応表
opフィールドとfuncフィールドが操作を指定している。rsはソースレジスタ、rtも通常はソースレジスタ、rdはデスティネーションレジスタと呼ぶ。
