13th LSI Design Contests・in Okinawa Design Specification - 2
2.How to calculate 8bits parity for BCH(15,7)
From now, Polynomial notation will be used to explain BCH coding and decoding algorithm.
Assume the 7 bit information is { u0, u1, u2, u3, u4, u5, u6}, then polynomial notation can be used to show the information such as eq (1). Here, the bit position n from 0 to 7 corresponds to the power of x such as xn.
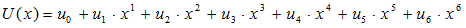 … (1)
… (1)
Then 15 bits code can expressed as eq (2).
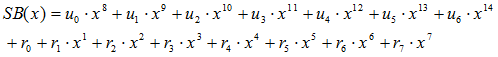 … (2)
… (2)
r0, r1, …, r7 bits are 8 bits parity as shown in Table 2. These parity coefficients are 0 to 7th power of x. and Information coefficients are 8 to 14th power of x.
Table 2: polynomial coefficients

Then once you calculate R(x) , SB(x) is easily obtained.
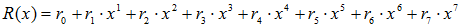 … (3)
… (3)
In BCH code, R(x) is remainder of U(x)*x8 divided by G(x).
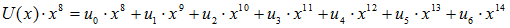 … (4)
… (4)
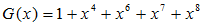 … (5)
… (5)
Here, G(x) is called as the generation polynomial.
U(x)*x8 in eq (4) means the coefficients u0, …, u6 are shift to higer bit by 8 bits. The order of G(x) is 8. The remainder R(x) will be order of 7 or less. However, please note that the calculation uses Garois field rule.
In reality, the remainder calculation is very easy. Using the equation (6) iteratively, polynomial with order more than 8 can be reduced to less than 7. The result of polynomial is the remainder polynomial.
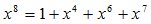 … (6)
… (6)
However, during this computation, addition and/or subtraction between coefficients shall be replaced by exor computation because of Grois field as shown in eq (7).
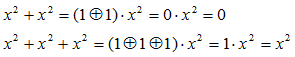 … (7)
… (7)
