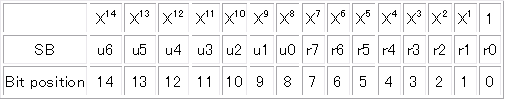
13th LSI Design Contests・in Okinawa Design Specification - 4
4.BCH decoder algorithm
Remember the generation polynomial of eq (5) is used in BCH(15,7) encoding.
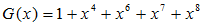 … (5)
… (5)
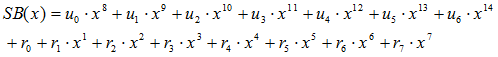 … (2)
… (2)
Since SB(x) is defined as eq (2), SB(x) can be divided by G(x), in other words, remainder is 0. Then we can judge if the remainder is 0, no error exists in a code. Actually, BCH(15,7) can correct 2 bit errors in 15 bits codes.
The generation polynomial G(x) can be thought G1(x)*G2(x) as shown in eq (9).
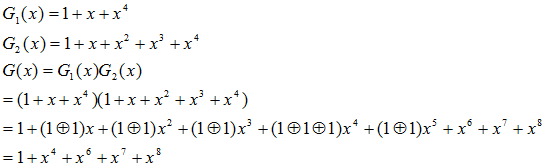 …(9)
…(9)
Then, SB(x) can be divided by either G1(x) or G2(x). If no error in a code, both remainder of G1(x) and G2(x) are both 0s.
[SB(x) is transmitted. Then RB(x) is received. If no error happened during transmission, RB(x) can be divided by both G1(x) and G2(x). Here we define Syndrome S1(x) = remainder of RB(x) divided by G1(x) , S2(x) = remainder of RB(x) divided by G2(x). Since both G1(x) and G2(x) is 4th order polynomial, syndromes are power of 3 or less polynomials as shown in eq (10).
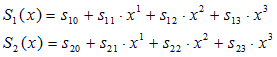 (10)
(10)
According to the coefficients (S10, S11, S12, S13) and (S20, S21, S22, S23), error status can be obtained. Since those coefficients are only 8 bits, then totally only 256 cases exists. Table 5 shows the relation between 8 coefficient bits and error status.
In table 5, YELLOW cell corresponds to syndrome = 0. This cell indicates no errors in code. BLUE cells are corresponds to 1 bit error. Totally 15 cells are blue cells. The number in the blue cell indicated the position of the error. The position is explained in table 6, which is the same as the power of xn. Since the error is bit error, error can be recovered by flip the value at the error position. The RED cell corresponds to 2 bit error. There are 15*14/2=105 cells. Each cell indicates two error position values. Other 135 empty cells are more than 3 bit errors. The error cannot be recovered.
Table 5: relation between 8 syndrome bits and error status
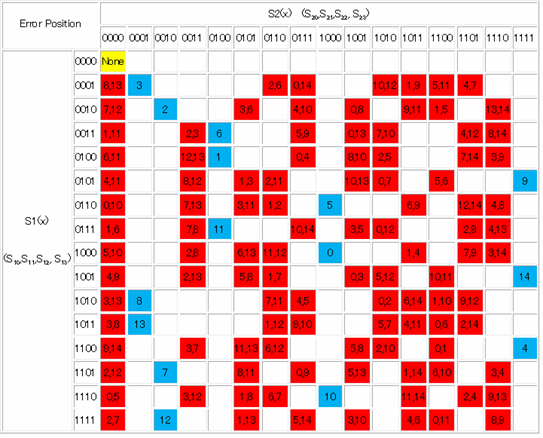
Table 6: error position indicator