Radix-2 algorithm

We talk about Radix-2 algorithm and butterfly computation. It shows fourier transform result of X(k) in last chapter.

(2.9)

(2.10)

(2.11)

(2.12)

Their formulas are coordinated of even or odd at sigma, as (3.1)

(3.1)

One FFT can divide two FFT at N even and N odd.

(3.2)

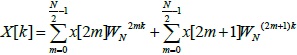
NIf N is power of 2, it can divide FFT and more. Finally, it divide several FFT(butterfly computation) of N=2. This is Radix-2 algorithm. Its algorithm usually reduce of calculation, reason of using complex adder-subtractor only.

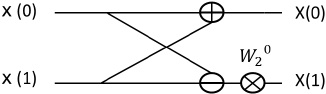
Fig.1 shows butterfly computation circuit using of butterfly computation.

Fig.1:  Butterfly computation circuit

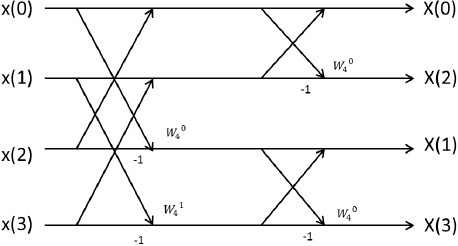
Fig.2 shows calculation flow about discrete fourier coefficient of N =4. Note,

under the arrow of -1 is subtraction, twiddle factor at the top of line is multiplication.

Fig. 2:   Conceptual diagram of 4 points FFT about Radix-2 algorithm

Calculated results used of are changed (3.3) ,(3.4), (3.5), (3.6). Their results equal DFT results.

(3.3)

(3.4)

(3.5)

(3.6)