3-3. Radix-2アルゴリズム

Radix-2アルゴリズムおよびバタフライ演算について述べる。 前章の、X(k) のフーリエ変換の結果を以下に示す。

(2.9)

(2.10)

(2.11)

(2.12)

これらの式を偶奇で分けてシグマでまとめると、(3.1)式のようになる。

(3.1)

このように1つのFFTはNの偶奇で分けて2つのFFTに分割することができる。

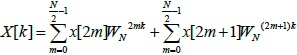
(3.2)

N が2の累乗であれば、その分割後のFFTもさらに分割できるため、最終的にいくつかの N=2 のFFT(バタフライ演算)まで分割できる。 これをRadix-2アルゴリズムという。Radix-2アルゴリズムにおいては、基本的には複素加減算だけで行えるため計算量を節約できる。

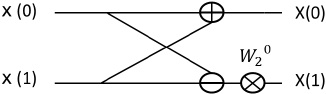
バタフライ演算を行う回路を表したものが、図1のバタフライ演算回路である。

図1:  バタフライ演算回路

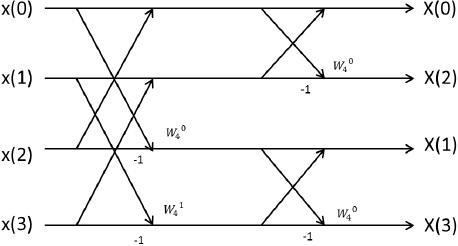
N=4 のときの離散フーリエ係数の計算フローを図示すると図2ようになる.

なお、矢印の下の -1 は減算、線の上部の回転因子は乗算を表している。

図2:  Radix-2アルゴリズムによる4点FFTの概念図

図に従って計算した結果は を用いると、(3.3), (3.4), (3.5), (3.6)式となり、DFTでの結果と等しいことが確認できる。

(3.3)

(3.4)

(3.5)

(3.6)