3-2. 高速フーリエ変換

高速フーリエ変換 (Fast Fourier Transform, FFT) とは、離散フーリエ変換を計算機上で高速に計算するアルゴリズムであり、1965年にジェイムズ・クーリーとジョン・テーキーによって提案された。

以下にアルゴリズムを示す。

例えば、N=4 のとき、離散フーリエ係数 X[k] は行列を用いて表現すると、(1.3)式のようになる。

入力列 X[k] を添字の偶奇で並び替えると、以下のように変形できる。

ここで、回転因子の性質について考える。 回転因子には周期性という性質があり、次の式で表される。

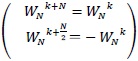
以下で (2.2) 式の証明を示す。

(2.2) 式の上式の左辺は、以下のように変形できる。

回転因子 の N 乗は

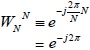
オイラーの等式 より、 となる。

よって

したがって

同様に計算すると、回転因子 のN/2乗は、

となるため、

となる。

(2.1) 式を、回転因子の周期性 を利用し、変形すると、

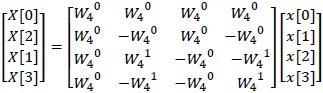
この係数行列(2.3)式には規則性があり、(2.4)式のように分解できる。

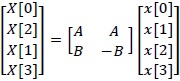
分解された係数行列(2.4)式は次のように変形できる。

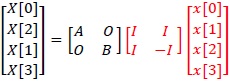
O は 2×2 の零行列 I は 2×2 の単位行列

(2.5) 式の赤文字で表された部分について計算すると、

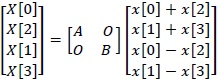
さらに計算を進めると(2.7)式になる。

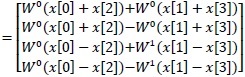
(2.7)式を展開すると、

計算結果(2.9), (2.10), (2.11), (2.12)式は、回転因子の周期性を利用し変形すると、3.1章の離散フーリエ変換の結果(1.4), (1.5), (1.6), (1.7)式と一致する。

N=4 のDFTは、16回の複素乗算と12回の複素加算が必要であるのに対し、(2.8)式から計算した場合、複素乗算4回と複素加算4回でフーリエ変換を実現できる。 このアルゴリズムを高速フーリエ変換と呼び、DFTに比べ、特に複素乗算の回数を大きく減らすことができる。

(16/10/07)　式(2.1)および式(2.7)に誤りがあったため訂正しました