4-1-1. N=4 の場合のFFT回路設計

(1) 回路設計

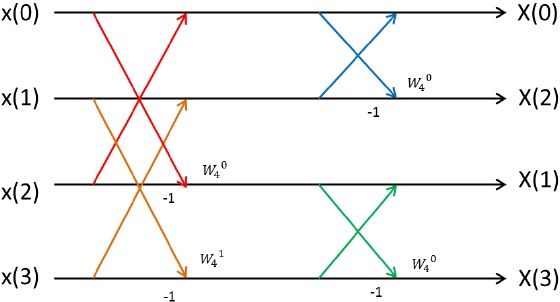
Radix-2アルゴリズムにより、1) N=4 のFFT演算の概念図は図3のようになる。

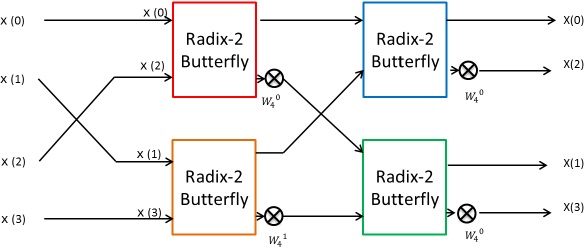
図3の概念図に従い、 N=4 のFFT回路は4個のバタフライ演算回路で実現できる。

概念的ブロック図を図4に示す。

図3の赤線により表されたバタフライ演算を図4の赤枠で表されたバタフライ演算回路へと変換する。 他の演算も同様である。

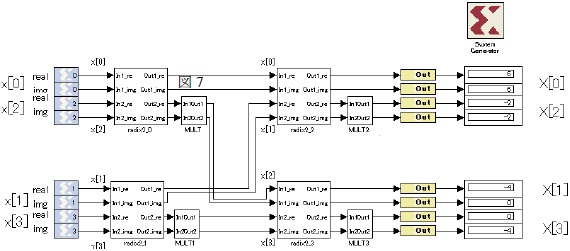
設計した回路を図5に示す。

各サブシステムの内部を以下に示す。

a）radix2

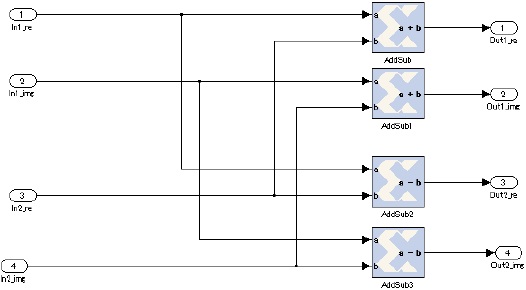
ここではradix2_0から3までの演算回路を示す。 2つの複素数を入力し、2つの複素数を出力する回路であるため、実数と虚数を分けて入力し、実数は実数同士、 虚数は虚数同士で加減算を行う回路である。構成は図4に示す。

図3のサブシステムradix-2_1、 radix-2_2、radix-2_3はradix2_0と同一の構成であるため省略する。

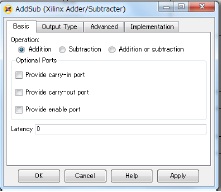
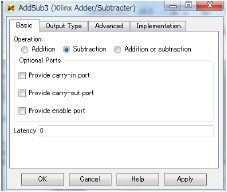
図6のAddSub1はAddSubと同一の構成であるため省略する。

同様にAddSub3はAddSub2と同一の構成であるため省略する。

b) MULT

ここではMULT0から3までの演算回路を示す。 MULTは回転因子乗算回路である。 複素数 、 の乗算は、 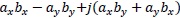と記述できる。

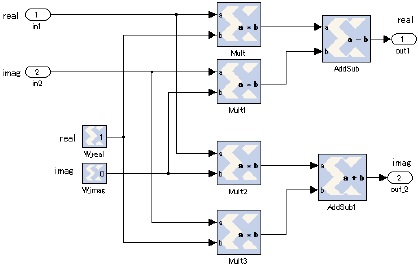
この過程に従って実数と虚数の2つの入力に対し、回転因子の実数と虚数を乗算する。 図5のサブシステムMULTのモデルを図9に示す。 図5のサブシステムMULT、MULT1、MULT2、MULT3のモデルはconstantブロックのパラメータ以外同一の構成のため、省略する。

図9のAddSubは図6のAddSub2と同一の構成であるため省略する。

同様に図9のAddSub3は図6のAddSubと同一の構成であるため省略する。

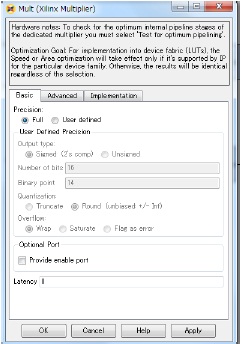
図9のMULTのパラメータを図10に示す。

図9のMult1、Mult2、Mult3はMultと同一の構成であるため省略する。

このとき回転因子は、 であるため、MULT、MULT1、MULT2、MULT3内の回転因子を表すconstantブロックのパラメータは表1のようになる。

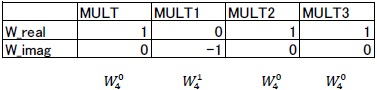
サブシステムMULTは、複素数の入力信号に対して、複素数の回転因子を乗算し、出力する回路である。

(2) 検証

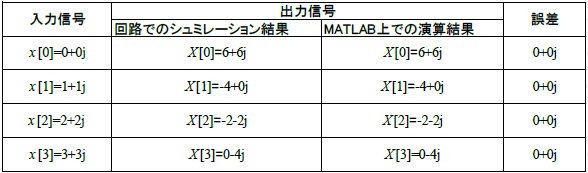
図5の回路に表2に示す値を入力して計算を行うと表2の X[0]〜X[3] を得た。

MATLABにおける演算結果（図11参照）と一致していることが確認できる。

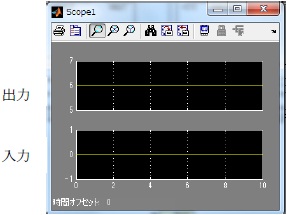
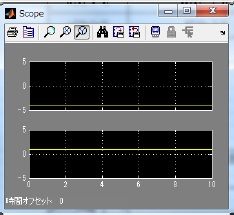
また、この回路の入力と出力をScopeを用いて確認すると、図12、13のようになる。

これからパラレル入力の場合のFFTのLatencyは 0 であることが確認できる。