4-1-2. N=8 の場合の回路設計

(1) 回路設計

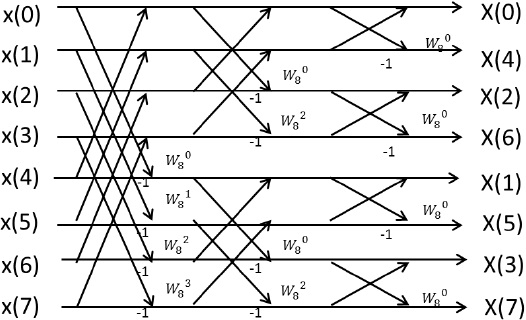
N=4 のときと同様、8点のFFTの概念図から概念的ブロック図を作成する。

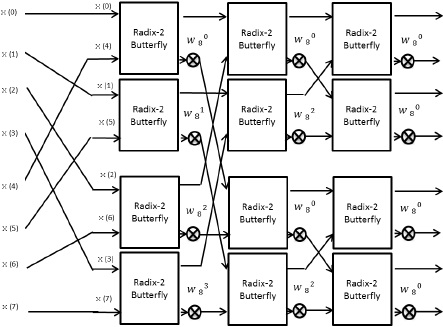
概念図に従い、N=8 のFFT回路は12個のバタフライ演算回路で実現できる。

概念的ブロック図を図15に示す。

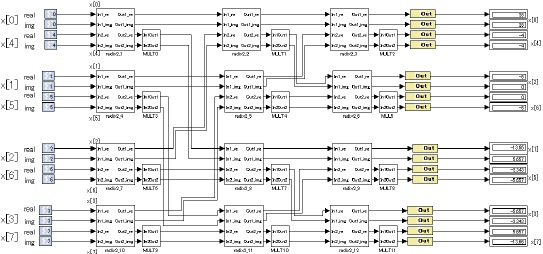
設計した回路を図16に示す。

サブシステムradix-2_1からradix-2_12までは図6のサブシステムradix-2_0と同一の構成であるため省略する。

サブシステムMULT0からMULT11も内部のconstantブロックのパラメータ以外は図7のサブシステムMULTと同じ構成であるため省略する。

このとき回転因子は, 、 、 、 であるため、MULT0から、MULT11内のconstantブロックのパラメータは表3のようになる。

表3のMULT3及びMULT9において、 を小数で表す際に概数として0.7071を用いた。

(2) 固定小数点演算での注意事項

サブシステムMULTのconstantブロックのビット幅は16ビット、小数点以下を表すビット幅は14ビットとする。 を小数点以下14ビットで表すと0.70709228515625となる。

浮動小数点で回路を構成すると回路規模が膨大となる。 そのため、一般的には固定小数を用いて演算を行う。 しかしながら、固定小数ではビット幅に制限があるため誤差が生じてしまう。

(3) 検証

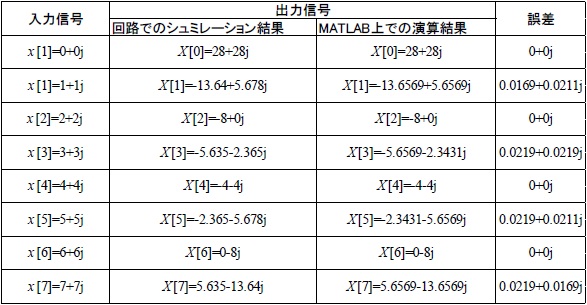
図9において、入力信号を x(0)=0+0j, x(1)=1+1j, x(2)=2+2j, x(3)=3+3j, x(4)=4+4j, x(5)=5+5j, x(6)=6+6j, x(7)=7+7j として回路上でシミュレーションを行ったところ、出力信号は X(0)=28+28j, X(1)=-13.64+5.678j, X(2)=-8+0j, X(3)=-5.635-2.365j, X(4)=-4-4j, X(5)=-2.3650-5.678j, X(6)=0-8j, X(7)=5.635-13.64j となった。 また、この回路の入力に対して出力が行われるまでのLatencyは0であった。

MATLABの演算結果との誤差を表4に示す。 誤差は 程度であり、この誤差の原因はサブシステムMULT内のconstantブロックにて を二進数で表した際に生じた丸め誤差である。 より精度の高い演算を行うには、サブシステムMULT内のconstantブロックの小数点以下を表すビット幅を増やす必要がある。