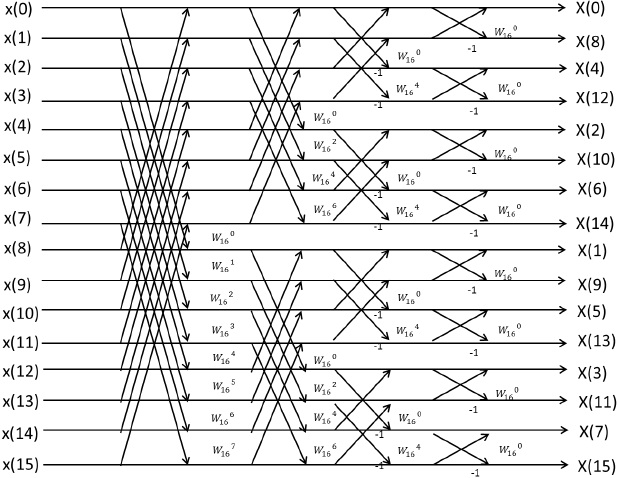
4-2-3. N=16 のFFT回路

(1) 回路設計

シリアル入力を遅延させバタフライ演算回路に入力し,出力信号のうちFFTに必要な信号のみ次のバタフライ演算回路へ送るようマルチプレクサで制御する。

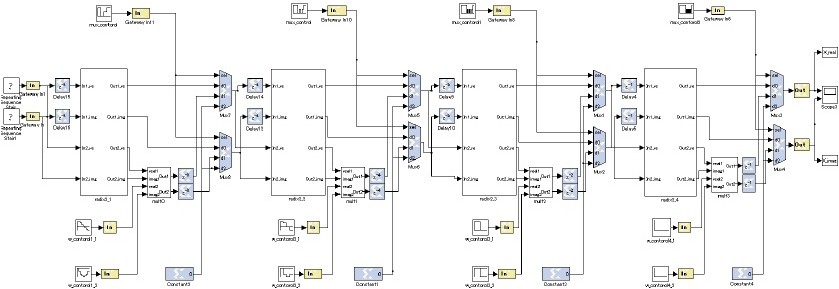
作成した回路を図34に示す。

1) MUX_control

MUX_controlというブロックはマルチプレクサのセレクタに入力する信号を制御するシーケンスであり、 これによりマルチプレクサの出力信号を決定している。

シーケンスのパラメータを図35に示す。

図35から読み取れるようにMUX_controlから出力される値はステップごとに変化している。 これによりバタフライ演算回路の出力信号のうちFFTに必要な信号のみ次のバタフライ演算回路へ送るよう制御を行っている。

2) W_control

W_controlは回転因子Wを表すシーケンスである。

STEPごとに複素乗算する回転因子の値(実部、虚部)を変化させて、バタフライ演算を行う。

回転因子Wは、 , , , , , , , であるため、シーケンスのパラメータは表9のようになる。

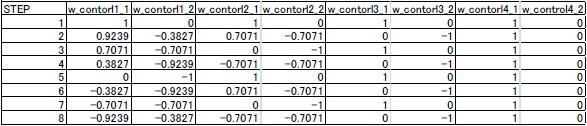
表9において, を小数で表す際に概数として0.7071、 を表す際に0.9239、 を表す際に0.3827を用いた。

表9からわかるように、図30のMULT0において最初のステップでは を乗算し、以降順に , , , , , , を乗算している。 MULT1において最初のステップでは を乗算し、次のステップでは を乗算している。 MULT2において最初のステップでは を乗算し、次に を乗算している。MULT3は常に を乗算している。

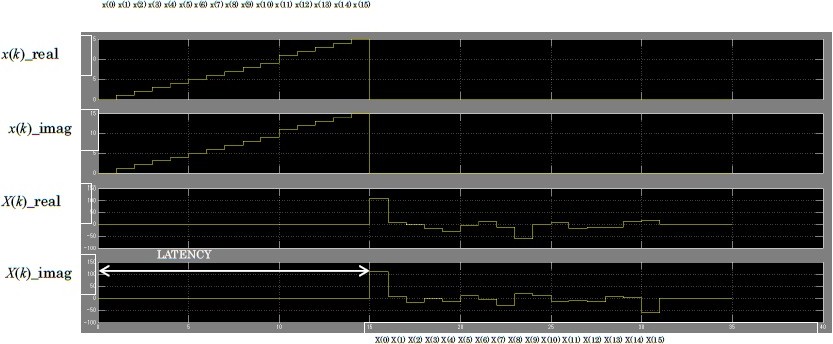
図34のシリアル入力に対する16点FFT回路のタイミングチャートを図36に示す。

(2) 検証

入力信号を x(0)=0+0j, x(1)=1+1j, x(2)=2+2j, x(3)=3+3j, x(4)=4+4j, x(5)=5+5j, x(6)=6+6j, x(7)=7+7j, x(8)=8+8j, x(9)=9+9j, x(10)=10+10j, x(11)=11+11j, x(12)=12+12j, x(13)=13+13j, x(14)=14+14j, x(15)=15+15j として回路上でシミュレーションを行った。 出力波形を図37に示す。

MATLABの演算結果との誤差を表10に示す。

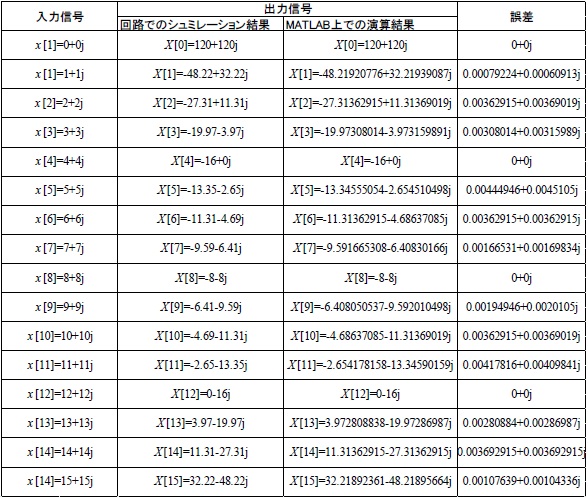
また、図37より、この回路の入力に対して出力が行われるまでのLatencyは15であることがわかる。

16点FFTの回路の検証については,検証用のmファイルを作成し,ランダムな入力に対し,MATLAB上でのFFT演算と、作成した回路におけるFFT演算の誤差を100回計測して、平均二乗誤差 (Mean Square Error, MSE) を求めた。 結果を表11に示す。

この検証により平均二乗誤差MSEが実部において 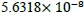、 虚部に の16点FFT演算回路が設計できたといえる。