| Japanese | English |

第14回LSIデザインコンテスト・イン沖縄 設計仕様書 - 3
3. 圧縮アルゴリスム
この章では、DCT/IDCT変換のアルゴリスムと量子化モジュール/逆量子化モジュールの詳細について説明します。 まず1D-DCTについて説明し、続けて2D-DCTについて述べます。
3.1. 1次元 離散コサイン変換 (1D-DCT)
1次元N点におけるDCPの公式は以下のようになります。
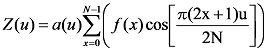
ただし u=0,1,2,...,N とし、α(u) は以下のように定義します。
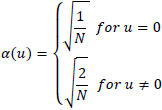
よって u=0 のとき、次式が得られます。
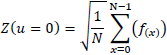
最初のDCT係数はサンプル数列の平均値です。 この値はDC係数と呼ばれ、それ以外の全ての値はAC係数と呼ばれます。
上記の方程式は行列の乗算として扱うことができます。
ここでXは入力行列とし、Cは変換行列、Zは変換されたDCT係数行列とします。また、tは転置を表します。 8×8の1D-DCTのとき、変換行列として式(5)が得られます。
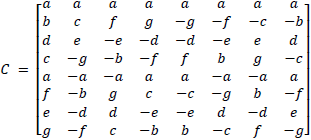
ただし、
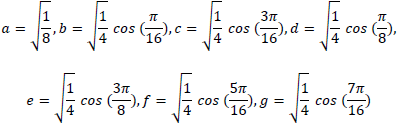
3.2. 1次元 逆離散コサイン変換 (1D-IDCT)
同様に、逆変換は以下のように定義されます。
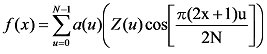
ただし x=0,1,2,...,N とし、α(u) は以下のように定義します。
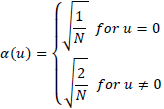
上記の方程式は行列の乗算として扱うことができます。
ここでXは入力行列とし、Cは変換行列、Zは変換されたDCT係数行列とします。
3.3. 2次元 DCT/IDCT
2D-DCTは1D-DCTの拡張であり、以下のように定義することができます。
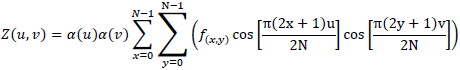
ただし u,v=0,1,2,...,N とし、α(u)とα(v)は式(2)によって定義されます。
逆変換は次式によって定義されます。
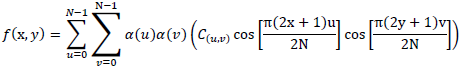
ただし、x,y=0,1,2,...,N-1とします。上記の2D-DCT計算は、以下のように分離して表すことができます。 したがって、次式のように表されます。
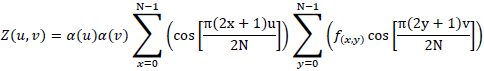
これは、2D-DCT計算が1D-DCTの水平成分の変換(行)と垂直成分の変換(列)によって達成できることを意味します。 この考え方について、グラフを用いて説明したものを図4に示します。
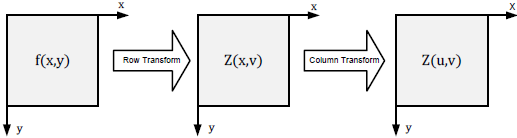
図4 1D-DCTを用いた2D-DCTの計算
行列演算によって、式(12)を用いることで2D-DCT変換は計算できます。
上記の考え方は逆DCTでも使用でき、次式のように表せます。
2D-DCT/IDCT変換の2段階計算を行うにあたり、その過程で重要なことがあります。 2回目の1D-DCT(またはIDCT)変換を行う際には、一回目の1D-DCT変換の結果を用いて計算することを忘れてはいけません。
3.4. 量子化と逆量子化
量子化のプロセスでは、DCT係数の全ての成分が、式(14)によって定義された 量子化テーブルQによって除算されます。
一般に量子化テーブルQは左上に低い数字を持ち、右下に近づくに従って値が増えていきます。 量子化テーブルの値は定められていないので、ユーザが任意に量子化テーブルを選ぶことが可能です。 しかしながらJPEG委員会が推奨している量子化テーブルQがいくつかあるので、 そのなかのQ50_LuminanceをQ50_Chrominanceを以下に示します。
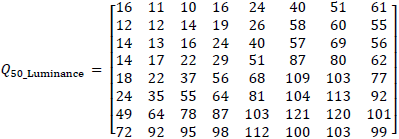
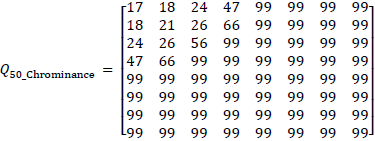
量子化テーブルを使用することで、 実行時間に対する圧縮レベルをカスタマイズできます。 ユーザがより良い圧縮率を得たいならば、より値の大きな量子化テーブルを使用しなければなりません。 しかし、より良い画質を得たいならば、値の小さな量子化テーブルを使用しなければなりません。 式(16)を用いて上記の基本的な量子化テーブルをスケーリングすることによって、 別の量子化テーブルを得ることができます。
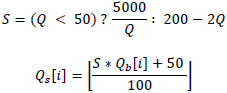
例として、Q=80における量子化テーブルをスケーリングしてみましょう。
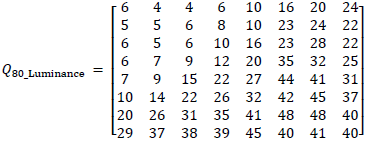

伸長モジュールの入力では、式(18)で定義されるようなIDCTモジュールへ入力する前に、DCT係数を逆量子化しなければなりません。